Прогнозування розвитку складних ймовірнісних систем (+ практика розрахунків)

Прогнози, побудовані на основі рядів динаміки параметрів складних ймовірнісних систем, зазвичай належать до пошукових формалізованих прогнозів, що ґрунтуються на виявленій тенденції

У науці є щось таке, від чого захоплює дух.
Володіючи дріб’язковими запасами фактів,
за допомогою науки можна висунути
неймовірне число гіпотез та припущень.

Марк Твен

Передбачення стану техніко-технологічного устаткування, прогноз погоди, врожайності сільськогосподарських культур дає змогу інженеру, фермеру, товаровиробникові завчасно приготуватися до них, урахувати їхні позитивні та негативні наслідки, а за можливості – втрутитись у процес розвитку і, що важливіше – управляти ними.

Рішення, які приймаються сьогодні, спираються на оцінювання розвитку явищ у минулому і, своєю чергою, так чи інакше впливають на майбутнє.

Основні поняття й методи прогнозування

Прогнозування (від грец. πρόγνωση – передбачення, пророкування) – це імовірнісне оцінювання майбутніх значень параметрів систем, що вивчаються і є важливою попередньою стадією їхнього управління.

Прогнозування – головна методологічна база для прийняття рішень у процесі управління будь-якими складними імовірнісними системами:

• природними;
• технічними;
• економічними;
• екологічними тощо.

Наукова обґрунтованість цієї бази стає особливо актуальною як у разі короткострокового, так і середньострокового чи довгострокового прогнозування сучасних явищ та процесів.

Методи прогнозування поділяють на:

• інтуїтивні;
• формалізовані.

Інтуїтивні методи застосовуються під час прогнозування розвитку дуже складних імовірнісних систем, коли врахувати всі важливі чинники неможливо. Найбільш популярними інтуїтивними методами прогнозування є методи експертного оцінювання.

Методи експертного оцінювання:

• індивідуальні:
  • аналітичне експертне оцінювання;
  • метод інтерв’ю;
  • парні порівняння тощо;
• колективні:
  • метод комісії;
  • метод Дельфі;
  • метод Патерн;
  • мозковий штурм та інші.

Формалізовані методи застосовуються під час прогнозування розвитку порівняно простих імовірнісних систем, коли всі важливі чинники піддаються обліку та вимірюванню. Початковим етапом прогнозування при цьому є формалізація інформації про попередній розвиток у період передісторії у виді певних кількісних показників і моделей. Довжина періоду передісторії (ряду динаміки або часового ряду) позначається N (таблиця 1), а довжина періоду попередження (прогнозування) – L.

Головними елементами ряду динаміки є рівні ряду Y_i та інтервали, або моменти часу, до яких вони належать.

В основі прогнозування лежить екстраполяція знайдених у часових рядах тенденцій, тобто поширення виявлених у період передісторії (на відрізку часу 1, 2 … N) закономірностей і зв’язків на майбутнє – на період попередження L.

Екстраполяція полягає в гіпотезі про інерційність розвитку систем, яка ґрунтується на припущенні, що в недалекій перспективі виявлені в минулому зв’язки та закономірності кардинально не зміняться і матимуть чинність певний час і в майбутньому. Таке припущення є реальним, особливо для короткострокового періоду, оскільки докорінні зміни показників більшості дієвих систем зазвичай потребують значних зусиль, коштів і тривалого часу.

Розрізняють точковий прогноз (у виді одного числа) та інтервальний прогноз (у виді двох чисел – нижньої та верхньої меж довірчого інтервалу).

Достовірність довірчого інтервалу Р зазвичай задається самим дослідником і є показником ймовірності потрапляння майбутнього фактичного значення прогнозованого параметра системи в інтервал від нижньої до верхньої межі.

Найпопулярніші в практичних задачах види прогнозування:

• 95%-й довірчий інтервал
  • рівень достовірності: Р = 0,95
  • вірогідність помилки: 1 – Р = 0,05
• 99%-й довірчий інтервал
  • рівень достовірності: Р = 0,99
  • вірогідність помилки: 1 – Р = 0,01
• 90%-й довірчий інтервал
  • рівень достовірності: Р = 0,90
  • вірогідність помилки: 1 – Р = 0,10

Є дві важливіші характеристики прогнозу:

• точність;
• достовірність.

Точність визначається шириною довірчого інтервалу, тобто різницею між верхньою та нижньою межами інтервального прогнозу. Що вища ця різниця (що ширший довірчий інтервал), то нижча точність прогнозу, і навпаки.

Найбільшу точність має точковий прогноз у виді одного числа, межі якого збігаються, а ширина дорівнює нулю.

Інтервальний прогноз менш точний у порівнянні з точковим, однак більш правдивий, оскільки достовірність Р визначається імовірністю потрапляння майбутнього значення прогнозованого параметра системи у довірчий інтервал.

Достовірність точкового прогнозу близька до нуля, оскільки будь-яке відхилення майбутнього фактичного значення від прогнозованого (точки на числовій осі) вважається помилкою прогнозу.

Доходимо висновку, що точність і достовірність прогнозу є характеристиками, які перебувають у зворотному зв’язку між собою: з підвищенням одного параметра інший параметр знижується, і навпаки.

Завдання дослідника полягає у знаходженні компромісу між точністю й достовірністю прогнозування.

З указаних позицій точковий прогноз є максимально точним і мінімально достовірним.

У процесі задання потрібних рівнів достовірності прогнозу (Р = 90%, 95%, 99%) дослідник підвищує ширину довірчого інтервалу, але при цьому його точність прогнозування знижується.

Завжди потрібно шукати компроміс між достатньою точністю та достовірністю оцінювання майбутнього стану параметрів досліджуваної системи.

Класифікація прогнозів

Прогнози класифікують за різними ознаками. Одну з можливих класифікацій наведено на рисунку 1.

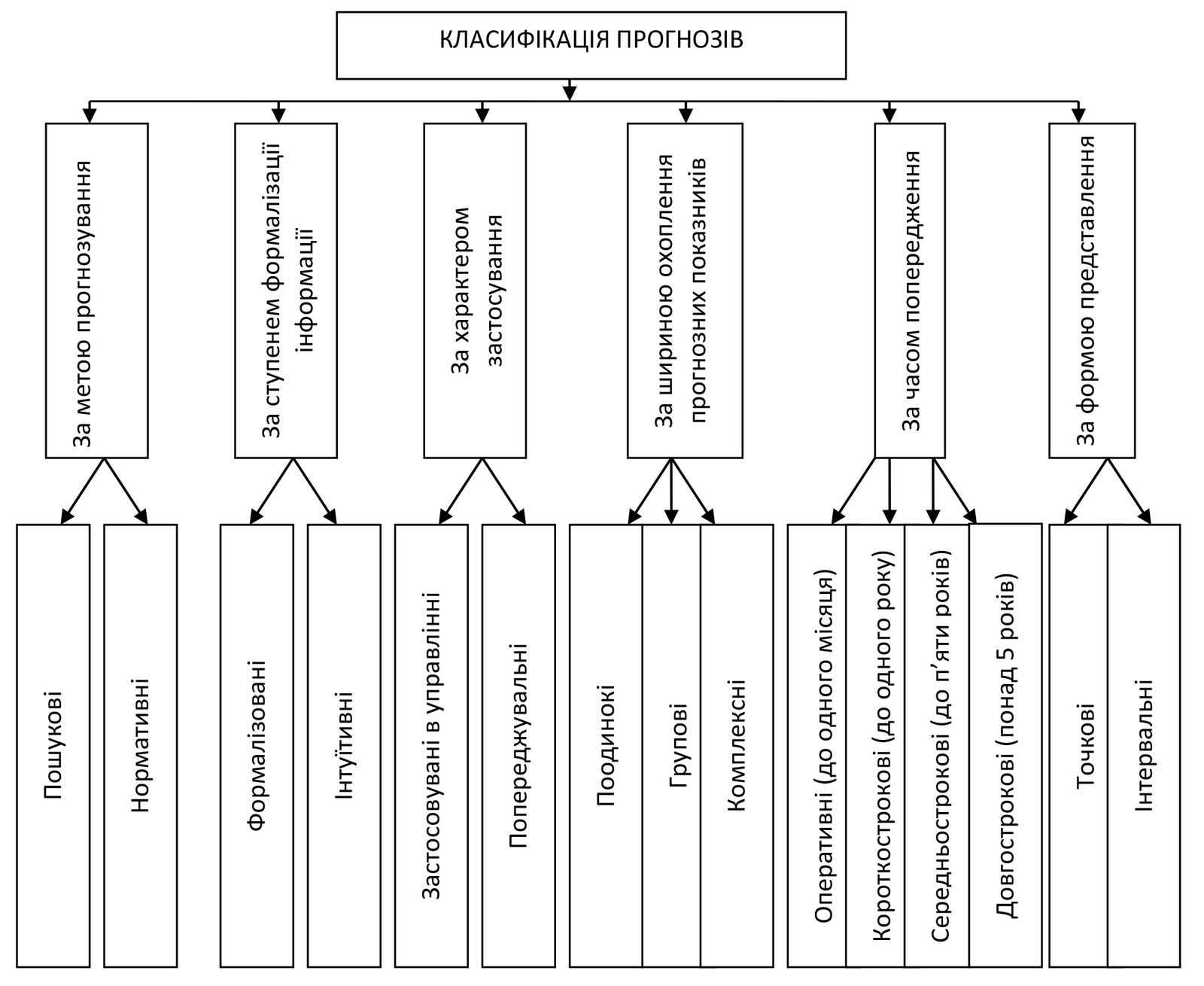
Прогнози, побудовані на основі рядів динаміки параметрів складних імовірнісних систем, зазвичай належать до пошукових формалізованих прогнозів, що ґрунтуються на виявленій тенденції.

Характерною особливістю попереджувальних прогнозів є використання схеми «якщо параметр системи досягне прогнозного рівня Х, то система опиниться в стані Y».

Що ж до інших ознак класифікації, то всі вони відрізнятимуться одна від одної у кожному конкретному випадку прогнозування.

Під час прогнозування можуть бути застосовані абсолютні, відносні та середні характеристики часових рядів (таблиця 2).

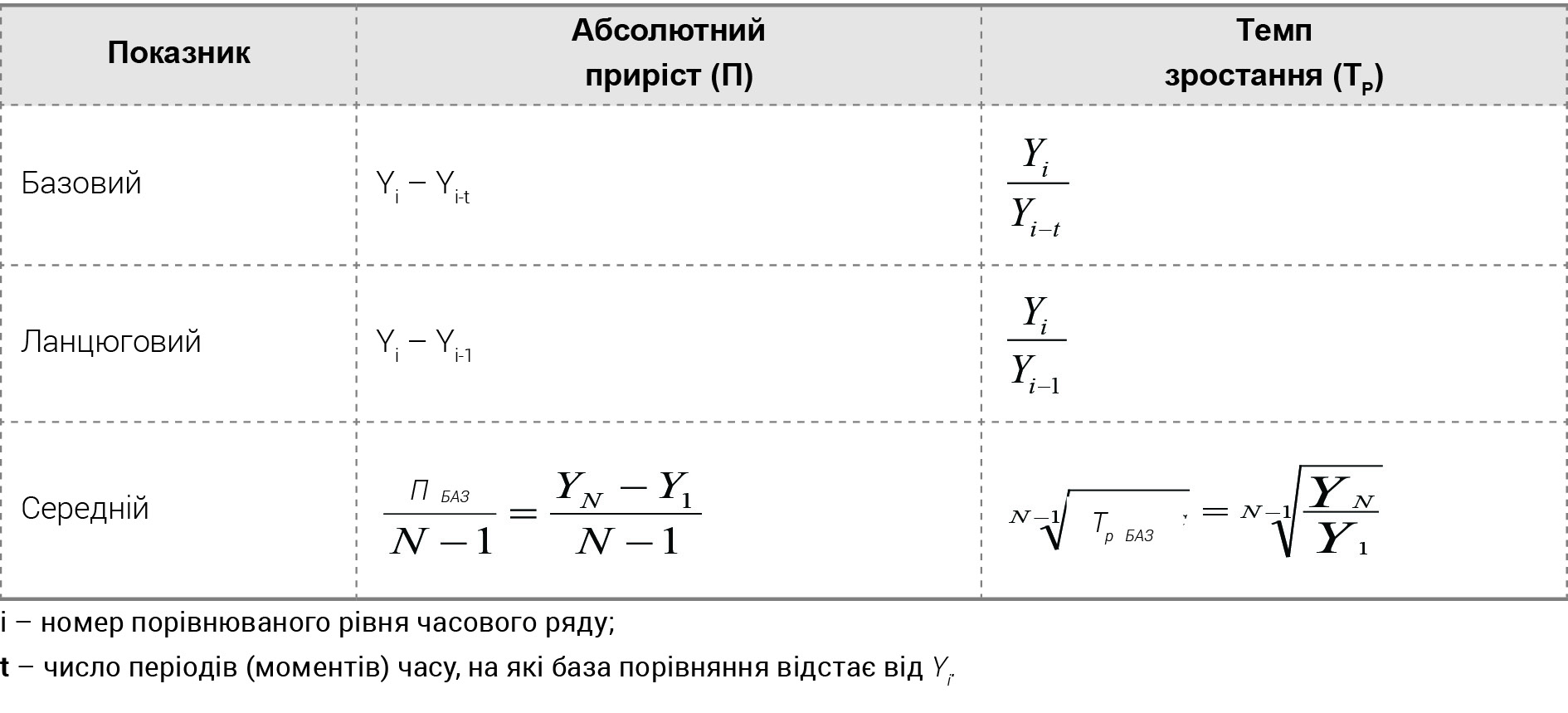
Так, знайдені на стадії попереднього аналізу середні показники динаміки можуть бути використані як найпростіші інструменти прогнозування.

Формула 2 зазвичай застосовується і дає хороші прогнозні результати у разі рівнопришвидшеного розвитку рівнів ряду динаміки, тобто коли він змінюється в геометричній прогресії.

Перевірка цієї умови зводиться до перевірки приблизної сталості ланцюгових темпів зростання (Тр_ЛАН ≈ const).

Прогнозування на основі трендових моделей

Побудовану на етапі аналітичного вирівнювання часового ряду трендову модель, що відбиває основну тенденцію розвитку рівнів ряду динаміки у часі Х, також часто використовують як інструмент прогнозування майбутніх значень досліджуваного параметра.

Точкові прогнози знаходяться на базі рівняння тренду шляхом підставляння замість Х майбутнього значення фактора часу Х = N + L, яке відповідає періоду попередження L.

Наприклад, для лінійного тренду Ŷ = a₀ + a₁Х точковий прогноз має такий загальний вигляд (формула 3):

Ŷ_{N + L} = a₀ + a₁(N + L).

Використання трендових моделей як інструментів прогнозування відкриває можливість отримати поряд із точковим прогнозом також й інтервальний прогноз у виді двох чисел – нижньої та верхньої меж довірчого інтервалу із заздалегідь заданою достовірністю Р потрапляння в нього фактичного значення Y_N+L.

Межі довірчого інтервалу прогнозу розраховують за такою загальною схемою (формула 4):

Ŷ_N+L ± Δ,

де Δ – гранична похибка прогнозу.

Формула 4 означає, що в центрі довірчого інтервалу перебуває точковий прогноз Ŷ_N+L, а ширина самого довірчого інтервалу дорівнює 2Δ.

У результаті отримання довірчого інтервалу за формулою 4 точність прогнозу знижується, оскільки розширюються його межі, але при цьому забезпечується заздалегідь задана достовірність прогнозу Р.

Далі постає запитання: як розрахувати величину граничної помилки прогнозу? Теорія статистичного моделювання та прогнозування дає на нього наступну відповідь.

Для лінійного тренду формула граничної похибки прогнозу з достовірністю Р = (1–α)×100% потрапляння в довірчий інтервал майбутнього фактичного значення прогнозного параметра має такий вигляд (формула 5):

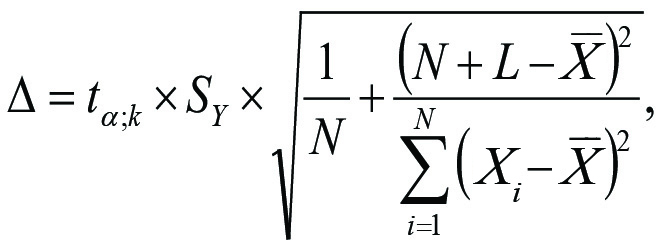
де:

• t_α;k – коефіцієнт довіри (α-квантиль t-розподілу Стьюдента з рівнем значущості α і k = N – m ступенями вільності; m – число оцінюваних коефіцієнтів тренду);
• S_Y – стандартна помилка тренду;

Слід зазначити, що рівень значущості α по суті є вірогідністю помилки й визначається, виходячи з необхідної й заздалегідь заданої достовірності Р (у %) з наступного співвідношення:

α = 1 – Р/100.

Наприклад, за необхідної достовірності потрапляння в довірчий інтервал майбутнього фактичного значення Y_N+L×Р = 95%×α = 0,05; за Р = 90% це становитиме 0,10; за Р = 99% це буде 0,01 тощо.

Число ступенів свободи k = N – m для лінійного тренду (m = 2) дорівнює N – 2. А величина коефіцієнта довіри (α-квантиль t-розподілу Стьюдента) знаходиться за допомогою редактора Excel (команда – стьюдраспобр (α; N – m) – Enter). Стандартна помилка тренду S_Y визначається за формулою 6:

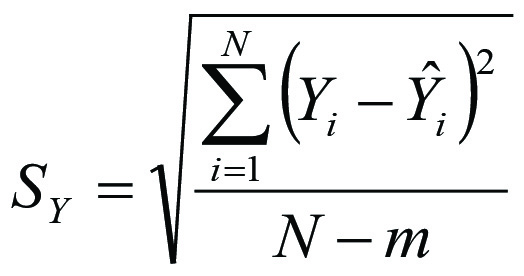
Розраховується стандартна помилка тренду S_Y автоматично у процесі побудови моделі тренду за допомогою стандартної програми «Регресія» редактора Excel.

Вона характеризує абсолютну точність знайденого рівняння тренду: що менше S_Y, то точніший тренд, і навпаки.

Третій співмножник (радикал) у формулі 5 відбиває обрану форму математичної залежності між рівнями ряду динаміки та часом Х. У цьому випадку для лінійного тренду вираз під коренем не надто складний, але у разі переходу до криволінійних функцій зв’язку він суттєво ускладнюється.

Так, за параболічної (2-го ступеня) форми тренду третій співмножник у формулі 5 набирає вигляду формули 7:

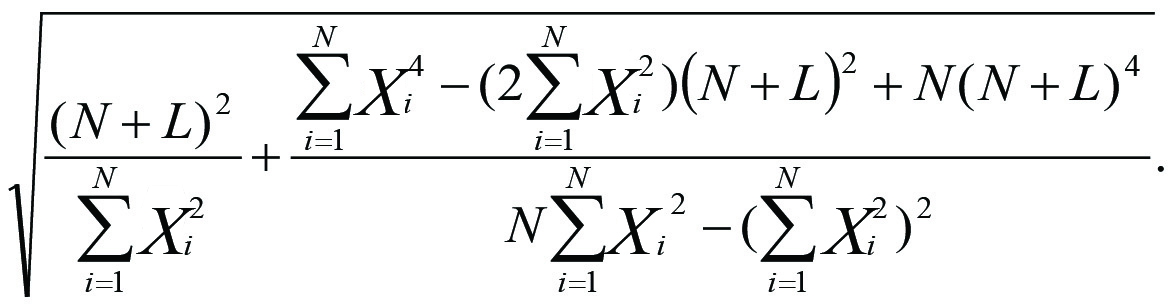
Слід пам’ятати, що автоматичний розрахунок величини граничної помилки прогнозу Δ у стандартних програмах кореляційно-регресійного аналізу редактора Excel не передбачений, а вручну здійснити вказані розрахунки за великих m практично неможливо. Тому у реальних дослідженнях під час прогнозування з цією метою користуються системою програм Statistica.

У процесі прогнозування майбутніх значень рівнів досліджуваного ряду економічної динаміки необхідно стежити, щоб поміж значень Y_i, що спостерігаються, не було так званих аномальних спостережень у виді піків або, навпаки, різких падінь рівнів ряду.

Річ у тім, що аномальні спостереження зазвичай свідчать про чинність якихось випадкових чинників, не характерних для інших періодів (моментів) часу. Тому за їхньої наявності середня величина Y буде спотворена і, як наслідок, коефіцієнти лінійного тренду a₀, a₁ міститимуть систематичну помилку. Це зрештою спричинить неправильну прогнозну оцінку, наприклад, сильно завищену чи занижену.

Є об’єктивні взаємозв’язки між числом оцінюваних коефіцієнтів тренду m і довжиною періоду передісторії N, а також між величиною N та періодом попередження L.

Доведено, що число N має у 3–4 рази перевищувати кількість оцінюваних коефіцієнтів тренду m.

Для лінійного рівняння m = 2, тому, щоб побудувати тренд Ŷ = a₀+a₁Х, необхідно мати щонайменше 6–8 рівнів часового ряду. А під час безпосереднього прогнозування має виконуватися умова L ≤ N/3, тобто довжина періоду попередження не повинна перевищувати третину довжини періоду передісторії.

Порушення зазначених співвідношень призводить до отримання ненадійних трендових моделей та, відповідно, до помилкових прогнозних оцінок.

Практика прогнозування

Розглянемо як приклад прогнозування на три моменти часу (L = 3) одного з параметрів хімічного агрегату на основі часового ряду наступних 12 спостережень (N = 12), що наведені в таблиці 3.

На базі даних таблиці 3 знайдемо ланцюгові, базисні та середні абсолютні прирости й темпи зростання рівня досліджуваного параметра (таблиця 4).

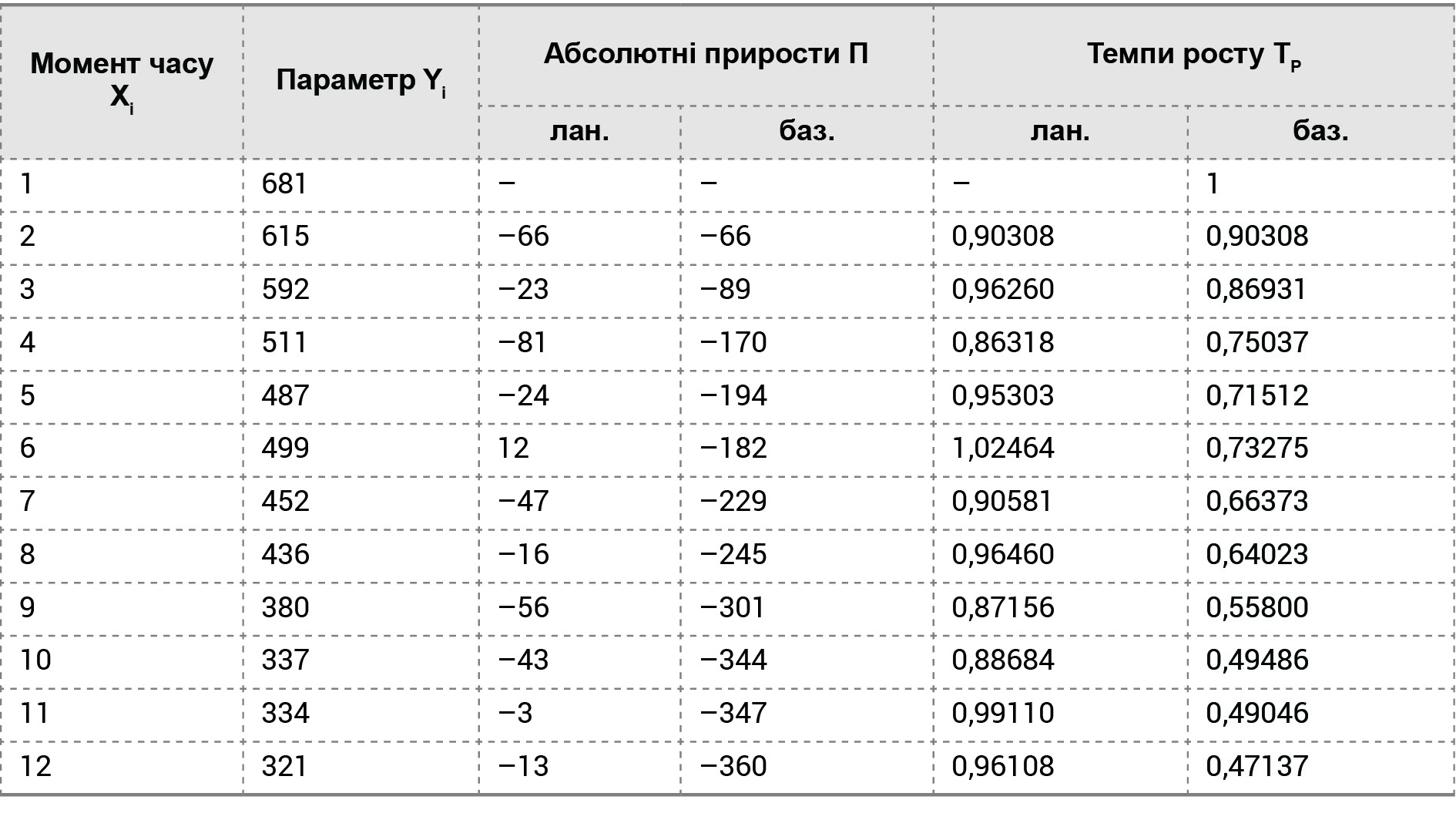
Середній абсолютний приріст:

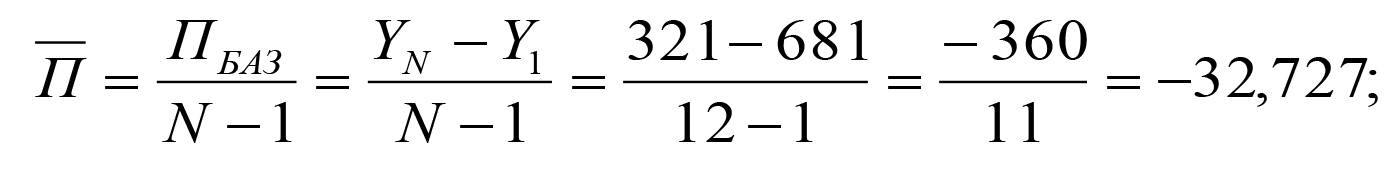
Середній темп зростання:

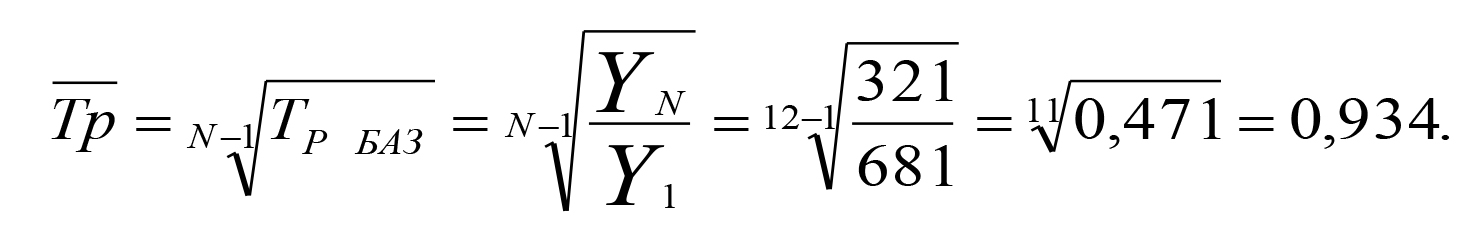
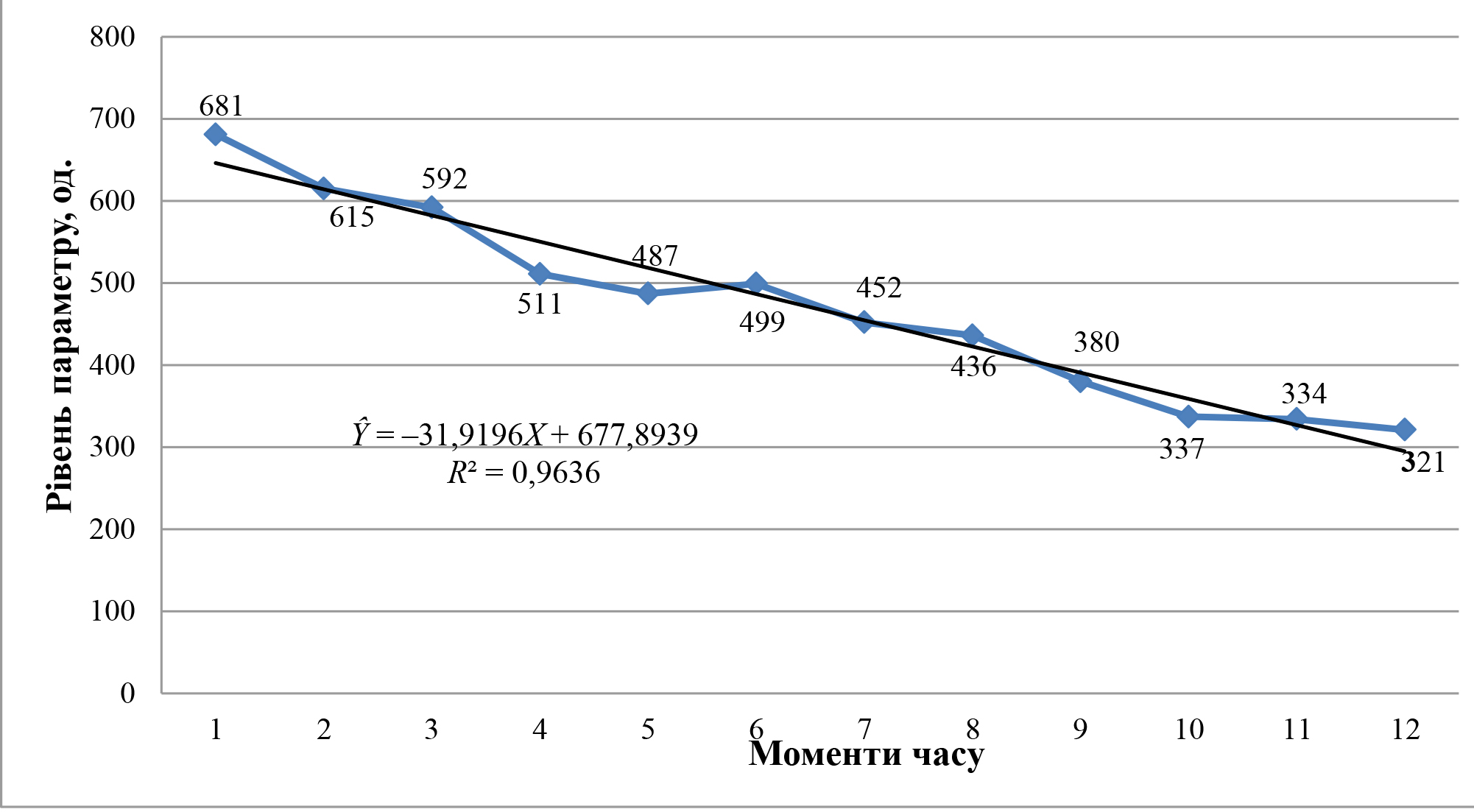
Отриманий лінійний тренд є достатньо точним: коефіцієнт детермінації R² = 0,9636 указує на те, що більше ніж 96% варіації досліджуваного параметра пояснюється саме його лінійною залежністю від часу.

Точковий прогноз за лінійним трендом знайдемо за формулою 3:

Ŷ_{N + L} = a₀ + a₁(N + L) = 677,8939 – 31,9196×(12 + 3) = 199,1.

95%-й довірчий інтервал прогнозу досліджуваного параметра на три моменти часу (L = 3) розрахуємо за формулою 4 з використанням системи Statistica, версія 10 (таблиця 5).

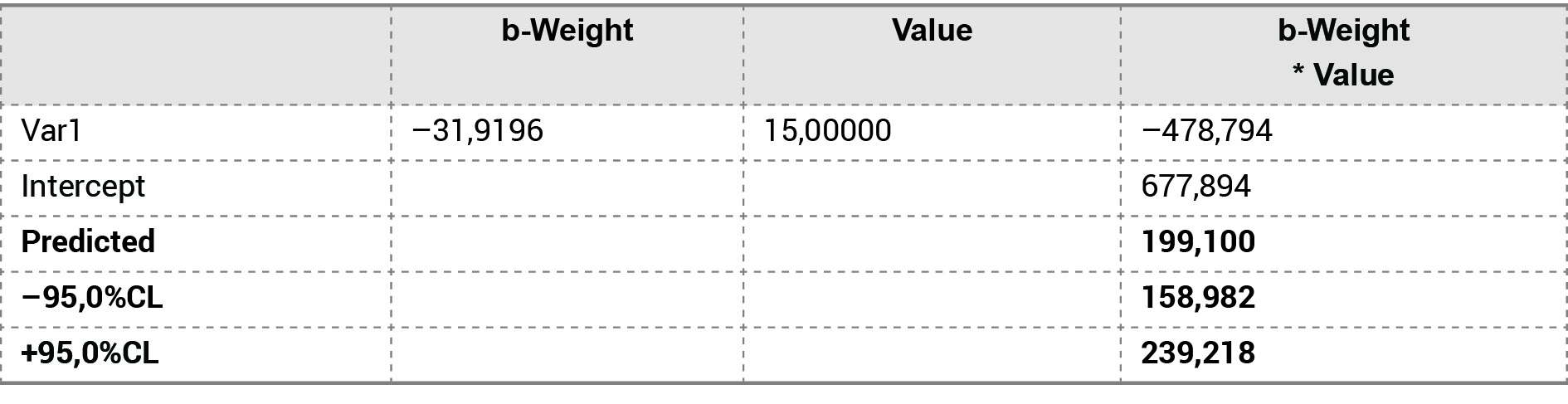
У таблиці 5 точковий прогноз (Predicted), нижня межа (–95,0%CL) і верхня межа (+95,0%CL) наведені в трьох виділених рядках (CL – confidence level – рівень довіри).

На рисунку 3 надано графічне зображення отриманих результатів прогнозування.

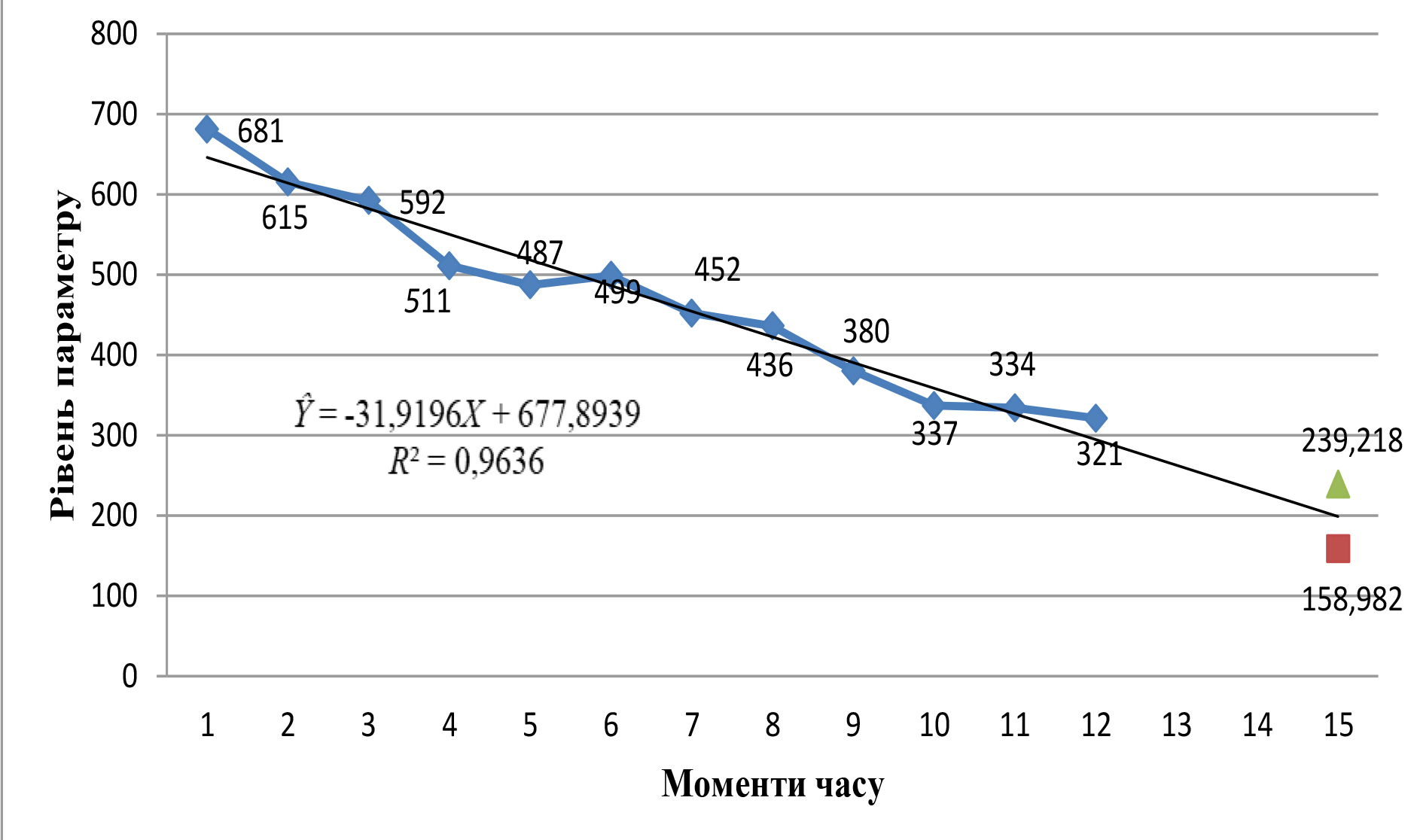
Таким чином, якщо закономірності й зв’язки, виявлені в періоді передісторії, збережуться певний час у майбутньому, то досліджуваний параметр хімічного агрегату слід очікувати у 15-й момент часу на рівні 199,1 од. При цьому з ймовірністю 95% можна стверджувати, що цей рівень перебуватиме у межах від 158,98 до 239,22 од.

У наступному номері журналу буде розглянуто методику комплексного прогнозування взаємопов’язаних параметрів складної імовірнісної системи на базі евристичного критерію балансу змінних з технічної кібернетики